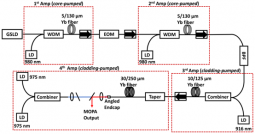
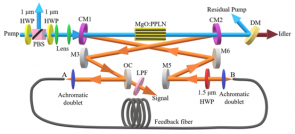
多芯光纤是一种新型光纤,这种光纤的包层中存在距离较近的多根纤芯,纤芯之间可产生较强的耦合,从而使各个纤芯内的光场成为一个整体,可用于光放大、脉冲压缩、超连续产生、光场调制、光子弹产生等过程。正六边形7芯光纤(横截面如图1),作为最常见的多芯光纤之一,可用于超连续产生[1],本篇文章通过数值模拟的方式,验证了普通的阶跃折射率7芯光纤可以产生超连续谱。

图1 正七边形7芯光纤横截面
作者假定不同纤芯之间仅仅存在线性耦合,从而得到了描述脉冲在7芯光纤中演化的耦合非线性薛定谔方程(式1,右边三行分别代表芯自身的色散、自身非线性和芯间线性耦合)。在线性情况下,该方程组的7个本征解代表在7芯光纤中能够稳定传播的7个超模式。每个模式在光纤中都有着不同的强度和传播速度,如图2所示,其中图2(a)表示电场强度在光纤中的分布,图2(b)表示每种超模式的传播常数,其中\beta(\omega)代表单模光纤传播常数,\kappa(\omega)代表线性耦合系数。

式1

图2 超模式分布及传播常数
当初始脉冲(脉冲宽度为100fs,功率15kW,中心波长1.55μm)输入到内芯(也就是图2(a)中的1号芯)时,作者讨论了纤芯间距对超连续产生的影响。在模拟中,所有芯径假设为6μm。
(1)若此时纤芯距离很近,芯距为12μm,纤芯与纤芯之间处于强耦合状态,脉冲演化如图3所示:第一行代表中间纤芯处脉冲在时域和频域的演化,第二行代表外围纤芯处脉冲在时域和频域的演化。由图可见,初始脉冲会迅速激发出低能量的模式A和高能量的模式F。然而,强耦合状态下模式A与模式F的传播速度差异很大,脉冲会迅速分裂成时间上不重合的两个孤子。模式A和F分别独立的进行自身的拉曼孤子自频移,并产生色散波(都是模式A,可能是A模式才满足相位匹配导致),且内外芯都能产生色散波,频率有略微差异)。由于模式F能量更高,模式F的红移量要大于模式A。

图3 强耦合内芯激发脉冲演化图
(2)若纤芯距离很远(改为25μm,其他参数均不变,如图4),纤芯与纤芯的耦合极弱,初始脉冲的大部分能量会保持在内纤芯。此时,光谱的演化与单模光纤如出一辙,仅当拉曼孤子红移到一定程度后,纤芯与纤芯的耦合因波长变长而增强,内纤芯的能量开始泄露到外纤芯中,峰值功率的减弱加上随波长增加而减小的非线性系数,拉曼孤子渐渐停止了红移。

图4 弱耦合内芯激发脉冲演化图
(3)当纤芯距离适中时(芯距15.5μm,如图5),纤芯与纤芯的耦合强度足够,模式A和模式F可在早期被激发出来,且不会因为较大的群速度差异而分离。这使得模式A和模式F能在时间上重合在一起,为模式间的能量转换提供可能。当处于模式F的频率1和处于模式A的频率2恰好群速度相同且相差13.2THz时,模式F的频率1便可作为泵光,借由拉曼增益将能量转移给模式A的频率2。因此,中等程度的耦合情况,模式F和A不仅自身在经历拉曼孤子自频移,模式FA之间也保持着拉曼增益的能量转换。在合适的传播距离下,F和A所对应孤子光谱的输出能量接近一致,结合色散波产生和两次四波混频过程,能形成较为理想的超连续谱。
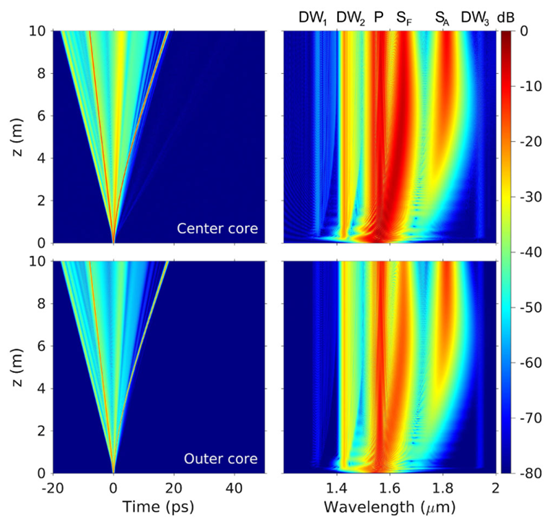
图5 中等耦合内芯激发脉冲演化图
若以光谱的加权标准差作为超连续产生光谱宽度的度量,则不同功率和芯距下内芯激发的光谱宽度如图6所示。
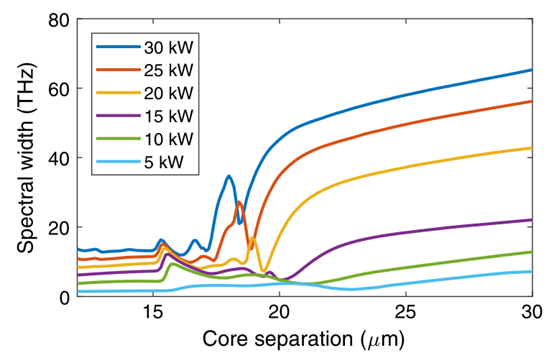
图6 内芯激发光谱宽度随功率和芯距的变化
与以上结果对比,作者还讨论了当初始脉冲(脉冲宽度为100fs,功率15kW,中心波长1.55μm)输入到外芯(也就是图2(a)中的2号芯)时的情况。作者发现,在三种耦合强度下,超连续谱的谱宽的整体规律与内芯激发一致,如图7所示,仅在弱耦合情况和强耦合情况有些许区别。

图7 外芯激发光谱宽度随功率和芯距的变化
在强耦合情况(激发芯2,芯距12μm)下,脉冲激发的模式有5个,能量被分散在5个群速度差异大,不会相互作用的模式里,整体的非线性强度减弱,故让光谱宽度小于内纤芯激发的情况。而对于弱耦合情况,由于外芯相邻的纤芯只有3个,少于内纤芯的6个。因此拉曼孤子自频移后期所出现的能量泄露相较内纤芯激发的情况要更小,故光谱宽度更大。
综上所述,利用多芯光纤的非线性效应可以产生超连续谱,光谱宽度由孤子拉曼红移和色散波产生主导,纤芯间的耦合可以产生孤子超模转换、芯间色散波产生、芯间四波混频等独特的非线性现象,从而影响超连续产生的光谱。纤芯之间的距离决定芯间耦合的强弱,芯距越小,耦合越强。强耦合区超连续产生的光谱随功率线性增加,弱耦合区近似于单模光纤,中等耦合区受孤子超模转换影响,光谱宽度随芯距波动,在特定芯距处存在极大值。
参考文献:
[1] Antikainen, G. P. Agrawal. Supercontinuum generation in seven-core fibers. Journal of the Optical Society of America B. 36(11):2927~2937.